




3D Vina chính thức phân phối các loại camera dùng cho kính hiển vi, máy đo 2D, máy đo 3D.
Sản phẩm chính hãng, giá rẻ nhất thị trường, demo miễn phí cho khách hàng cần sử dụng và thay thế camera

- Sửa chữa UPS , bộ lưu điện APC, Santak, Eaton Powerware, Emerson, Power Tree, Sunpac, Riello, Socomec…
– Kiểm tra đánh giá acquy, mua bán thanh lý UPS cũ các loại tận nơi.
– Sửa chữa biến tần các hãng Siemens, Abb, Schneider, Fuji, LS, Delta, Yaskawa, Mitsubishi, Simovert ……
– Các dịch vụ bảo trì, bảo hành mở rộng UPS, biến tần…
3D Vina cam kết có giải pháp khắc phục sự cố UPS để phục hồi hệ thống IT trong vòng 2h-4h
– Liên hệ ngay Zalo 0902 145 345 – Mr. Phong hoặc gọi trực tiếp.

About Leica Microsystems
Leica Microsystems develops and manufactures microscopes and scientific instruments for the analysis of microstructures and nanostructures.
3D Vina phân phối các loại kính hiển vi Leica trên thị trường Việt Nam, hàng chính hãng.

Liên hệ với Hiệu chuẩn 3D ngay khi Quý khách hàng cần mua Kính hiển vi công nghiệp, sinh học Shodensha.
Tất cả mọi nhu cầu được thỏa mãn ngay lập tức.
Kỹ thuật viên luôn túc trực để trả lời câu hỏi của Quý khách hàng


Liên hệ với Hiệu chuẩn 3D ngay khi Quý khách hàng cần mua kính hiển vi-máy đo Nikon và phụ kiện của Nikon.
Tất cả mọi nhu cầu được thỏa mãn ngay lập tức.
Kỹ thuật viên luôn túc trực để trả lời câu hỏi của Quý khách hàng – Hỗ trợ sửa chữa ngay khi Quý khách hàng cần hỗ trợ
Thông tin sản phẩm xem tại đây:

Liên hệ với Hiệu chuẩn 3D ngay khi Quý khách hàng cần mua kính hiển vi-máy đo OLYMPUS và phụ kiện của OLYMPUS.
Tất cả mọi nhu cầu được thỏa mãn ngay lập tức.
Kỹ thuật viên luôn túc trực để trả lời câu hỏi của Quý khách hàng

The COORD3 comprehensive Coordinate Measuring Machine range offer advanced measuring platforms from a budget bench-top CMM for small part inspection to some of the largest Gantry CMMs every produced. COORD3 CMMs are in active service throughout aerospace, defense and heavy equipment industries.
3D Vina là đại lý chính thức của thương hiệu máy đo CMM Coord3 Metrology tại thị trường Việt Nam.
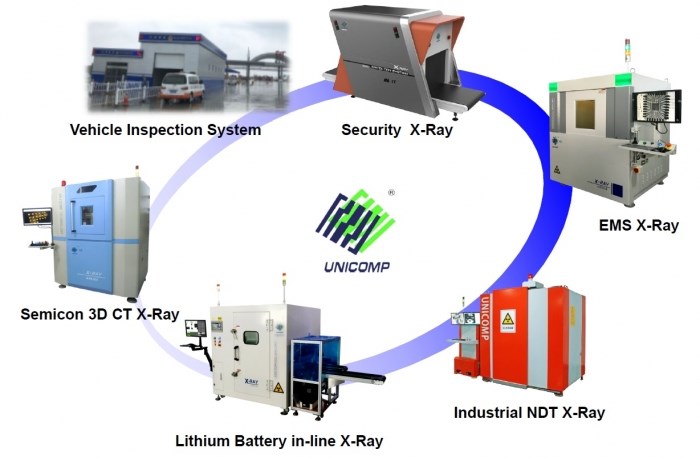
Company scale: Right now we have three factories in China, headquarter locates in Wuxi city with over 40,000sqm factory which mainly produce micro X-ray for electronics, our Shenzhen plant (5000 sqm) produce X-ray for lithium battery industry ( both Panasonic and Sony are our customer), our Chongqing factory (9000 sqm) produce the NDT X-ray for casting parts/pressure vessels/pipelines, etc.
Qualification: Unicomp company is certified with ISO9001, ISO14001, ISO27001 and OHSAS18001 by BSI, Unicomp X-Rays are complied with CE, FDA and Chinese GB standards.
Application: Unicomp X-ray machines are widely used in automotive parts, military industry, electronics, lithium battery, aerospace and national defense. Unicomp NDT x-rays are used for BMW, Audi, Volkswagen and other Chinese domestic brands automotive parts.
3D Vina cung cấp máy x ray công nghiệp Unicomp và làm dịch vụ sửa chữa, bảo dưỡng máy x ray tại thi trường Việt Nam

Liên hệ với Hiệu chuẩn 3D ngay khi Quý khách hàng cần mua thiết bị đo lường – Máy đo 2D, 3D CMM Hexagon và phụ kiện của Hexagon.
Tất cả mọi nhu cầu được thỏa mãn ngay lập tức.
Kỹ thuật viên luôn túc trực để trả lời câu hỏi của Quý khách hàng
Whether you are looking for an entry-level model or already have experience with coordinate measurement systems and are now looking to improve quality assurance or increase inspection capacity – we have the products and expertise you require.
Thông tin chi tiết sản phẩm xem tại đây:
https://www.hexagonmi.com/products/coordinate-measuring-machines
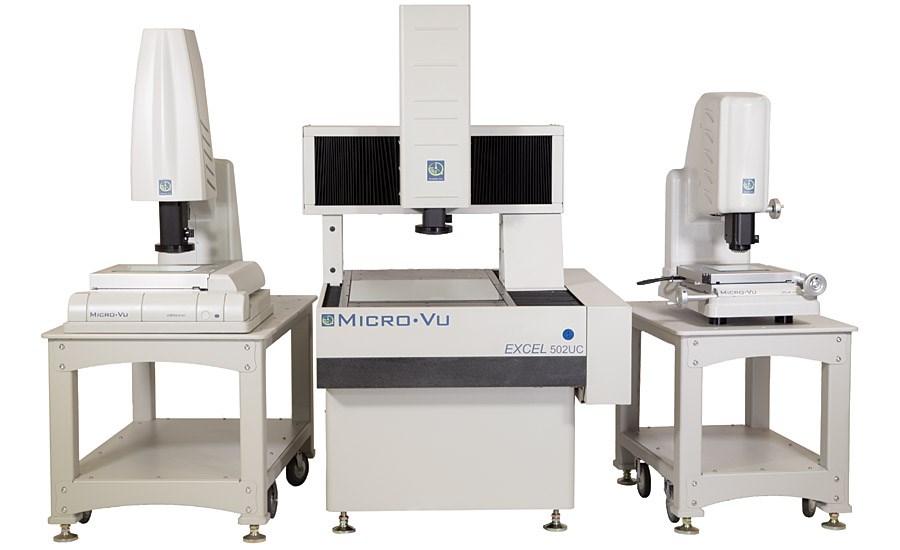
Liên hệ với Hiệu chuẩn 3D ngay khi Quý khách hàng cần mua Máy đo 2D, 3D Micro Vu và phụ kiện của Micro Vu.
Tất cả mọi nhu cầu được thỏa mãn ngay lập tức.
Kỹ thuật viên luôn túc trực để trả lời câu hỏi của Quý khách hàng

Unimetro Precision Machinery Co., Ltd is a professional manufacturer offering full line metrology products, including vision measurement machine, 3D coordinates measuring machine, profile projectors, tool microscopes, hardness testers etc, also we are manufacturing all the core components of the above products.
3D Vina xin trân trọng thông báo 3D Vina là nhà phân phối chính hãng của UNIMETRO tại Việt Nam.
Với sự hỗ trợ từ nhà sản xuất UNIMETRO, 3D Vina sẽ cung cấp giải pháp tổng thể từ thiết bị cho đến phụ tùng, đò gá máy đo 2D, máy đo 3D, máy đo CMM

Liên hệ với Hiệu chuẩn 3D ngay khi Quý khách hàng cần mua thiết bị đo lường – Máy đo CMM Accretech và phụ kiện của Accretech
Tất cả mọi nhu cầu được thỏa mãn ngay lập tức.
Kỹ thuật viên luôn túc trực để trả lời câu hỏi của Quý khách hàng

At the beginning of 2018, we developed Precise series CMM which with the 0.35+L/500 um accuracy, TOP series universal tool measuring machine (on-site type CMM without pressure air source) and online automatic testing products.
3D Vina là đại lý chính thức của thương hiệu máy đo CMM NANO Metrology Co., Ltd tại thị trường Việt Nam

3D Vina – Công ty chuyên về hiệu chuẩn thiết bị đo lường – sửa chữa – bảo dưỡng – hiệu chỉnh máy đo 2D, 3D, CMM, X ray.
3D Vina trân trọng ra mắt SÀN THƯƠNG MẠI – TRAO ĐỔI MUA BÁN MÁY ĐO CŨ – MỚI.
Rất mong quý khách hàng ủng hộ 3D Vina bằng việc cung cấp nhu cầu mua máy và nhu cầu bán máy cho 3D Vina.
Quá trình giao dịch qua 3D Vina vô cùng tiện lợi, do 3D Vina có đội kỹ thuật hỗ trợ việc di chuyển, lắp đặt, đào tạo, hiệu chỉnh và hiệu chuẩn máy đo
Nhà tài trợ nguồn máy đo 2d, máy đo 3d, máy đo CMM cho 3D Vina: ![]()

Liên hệ với Hiệu chuẩn 3D ngay khi Quý khách hàng cần mua thiết bị nội soi công nghiệp Dellon.
Với các đặc điểm nổi trội:
Tất cả mọi nhu cầu được thỏa mãn ngay lập tức.
Kỹ thuật viên luôn túc trực để trả lời câu hỏi của Quý khách hàng.
Thông tin chi tiết sản phẩm xem tại đây:

Liên hệ với Hiệu chuẩn 3D ngay khi Quý khách hàng cần mua thiết bị đo lường – Máy đo 2D, 3D VMS và phụ kiện của Rational.
Tất cả mọi nhu cầu được thỏa mãn ngay lập tức.
Kỹ thuật viên luôn túc trực để trả lời câu hỏi của Quý khách hàng
Products More>>
1. Profile Projector Series
CPJ-3000A/AZ series digital profile projector is an ergonomic and reliable measuring instrument…
2. Video Measuring System Series
Used in 2D measurement as well as 3D measurement,
this instrument is a high…
3. Coordinate Measuring System Series
Coordinate Measuring System (CMS) can be used
as measuring various…
4. Tool Microscope Series
Tool Microscope features multi-data measurement,
magnification, display, input…
5. Metalloscope Series
This instrument has two sighting systems: eyepiece
system and image system, which can be used to…
6. Tool Presetter Series
Integrating optics, machinery, electronics and video, Tool
Presetter is widely used in machine tool, machining…
7. White Light Interferometer Series
Combining with microscope and interferometer, this
instrument is suitable for…
8. Height Measuring Instrument Series
Based on precise machinery, modern sensor
technique and electronic…

Liên hệ với Hiệu chuẩn 3D ngay khi Quý khách hàng cần mua thiết bị đo lường và phụ kiện của Mitutoyo.
Tất cả mọi nhu cầu được thỏa mãn ngay lập tức.
Kỹ thuật viên luôn túc trực để trả lời câu hỏi của Quý khách hàng

3D Vina chính thức phân phối các loại camera, kính hiển vi điện tử, máy đo 2D, máy đo 3D, máy đo CMM từ Trung Quốc.
3D Vina với lợi thế nhiều năm kinh nghiệm làm dịch vụ hiệu chuẩn, sửa chữa, bảo dưỡng máy đo 2D, máy đo 3D, máy đo CMM, chính thức mở dịch vụ mua hàng từ Trung Quốc về cấp cho nhà máy.
Khách hàng cần => 3D Vina mua và bảo hành 1 năm cho tất cả thiết bị